Self-assembled polymer and surfactant systems can take milliseconds or longer to reach equilibrium. The typical size of the self-assembled aggregates (micelles) is from tens to thousands of molecules, or even higher. These two factors combine to provide a significant challenge, if one is to investigate the collective behavior of large numbers of molecules, and the structures that they spontaneously form at equilibrium. The surfactant systems form "complex fluids" that have rich phase behavior due to the wide variety of aggregate microstructures that they form. In this thesis, these challenges are met by adopting a simplified lattice model, in which the intermolecular and intramolecular interactions are reduced to a single interaction parameter. As a result of this simplification, the simulation model cannot be quantitatively compared with any real physical systems. However, once the simplification is made, the model can be solved exactly via computer simulation. The simulated behavior can then be qualitatively compared with real world systems. The detailed information provided by the simulation can produce valuable insights into the behavior of real world self-assembled systems that would be difficult to gain by any other means. The only inputs to the computer simulation are the structure of the molecules and their interactions, the concentrations in the system, and its temperature. No assumptions need to be made a priori about the aggregate sizes or shapes. An alternate form of the general reptation algorithm is developed for moving polymers in lattice Monte Carlo simulations. This algorithm is shown to be ideal for simulating polymer and surfactant systems. The computational efficiency of the algorithm is shown to increase with system density, in contrast to earlier algorithms that slow down dramatically in dense polymer systems. This new algorithm is rigorously tested by simulating two-dimensional athermal polymer systems (good solvent conditions). The new algorithm is shown to quantitatively reproduce known polymer dimensions - to an accuracy of better than one part in a thousand. The algorithm is then used to investigate the self-segregation of two-dimensional polymers in concentrated solutions or melts (Fig.1).
|
|
Fig. 1 A melt of 50-bead athermal polymers at equilibrium on the two-dimensional triangular lattice. The polymer segment density is 0.99. The polymers are shown as connected beads in the presence of a good solvent (open circles). The dimensions of the highlighted polymer are within 2% of the average values for R and Rg. The excluded volume condition is applied. |
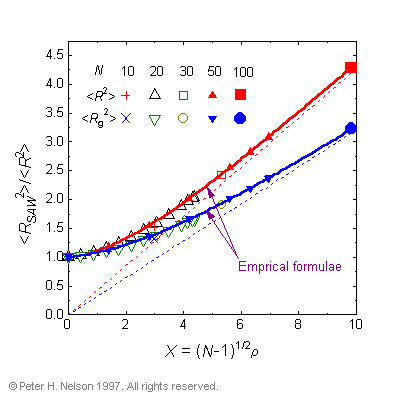
This collective behavior cannot be explained by traditional polymer theories that neglect the effects of excluded volume in concentrated systems. The segregation is caused by entropic effects that occur because of the excluded volume condition. The dimensions of the polymers are determined throughout the whole concentration range and new empirical formulae are provided for the polymer dimensions as a function of both concentration and polymer length (Fig. 2).
|
|
Fig. 2 Fits of the proposed empirical scaling relations to the mean-square dimensions of the polymers as a function of both concentration and length. The solid curves are least-squares fits to the simulation data for N=50. The straight lines indicate the extrapolated values for the existing scaling relation, which is only valid for large X. |
These are the first formulae that successfully predict the dimensions of polymers of finite length at all concentrations.
The simulation model is then extended to three-dimensional systems and energetic interactions are added. The conformations and self-assembly of (AB)n star block copolymers in dilute aqueous solution are investigated. The A and B blocks in each arm can be either hydrophilic (water loving - pewter) or hydrophobic (water hating - red). The hydrophobic-core stars, in which the inner blocks are hydrophobic and the outer blocks are hydrophilic, are found to behave as predicted by current theoretical models. However, hydrophilic-core stars (Fig. 3),
|
|
Fig. 3 A typical conformation of a 42-arm hydrophilic-core star at a c -value of 0.5. Each arm of the star is an AB diblock copolymer with NA=20 hydrophilic beads (pewter) and NB=20 hydrophobic beads (red). The axes indicate the center of the star. |
in which the inner blocks are hydrophilic and the outer blocks are hydrophobic, are found to behave in a manner incompatible with current theoretical treatments. The outer hydrophobic blocks aggregate into one or more globules away from the center of the star, thus breaking the spherical symmetry assumed in the theoretical models (Fig. 4).
|
|
Fig. 4 A typical three-globule conformation of a 42-arm hydrophilic-core star at a c -value of 2.5. |
Entropic effects in the core of the star cause the globules to separate from one another so that the three-globule conformation (Fig. 4) has a planar triangular arrangement of the globules, with the star’s center located in the middle of the triangle.
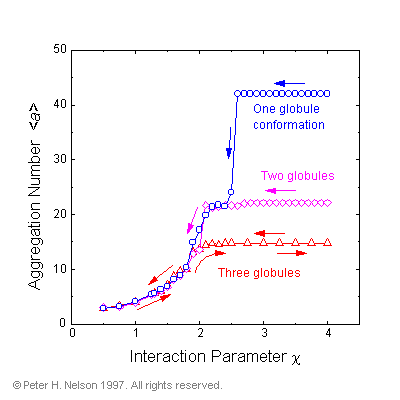
Specially prepared, low-energy, single-globule conformations, of the forty-two armed hydrophilic-core star were also investigated. It was found that while they were stable at low temperatures (high c), they underwent a spontaneous and irreversible decomposition into two-globule and then three-globule conformations as the temperature was raised (Fig. 5).
|
|
Fig. 5 Average aggregation number (no. of arms in a globule) from simulations of specially prepared 42-arm hydrophilic-core stars with one-, two-, and three-globules (at high c -values). The system followed the paths of the arrows. Irreversible decomposition of the one- and two-globule conformations is illustrated. |
This type of star polymer has not yet been synthesized, but has been shown to have many interesting properties. It shows potential for use in a number of diverse areas. In separation processes, drug delivery and other biological applications, its properties as a macromolecular amphiphile could prove useful. The molecule can undergo a dramatic change in size as the temperature is increased (or the solution conditions changed) so that it has potential applications as a viscosity modifier. Finally, because of the well-defined shape of the multi-globule conformations, these molecules should form ordered condensed phases whose structures may be selected by changing the architecture of the molecule. For example, changing the number of arms could cause a transition from lamella to cylindrical morphology. In this way, polymeric materials with a predetermined microstructure might be designed a priori.
It is now widely accepted that the micelles, which form in dilute surfactant solutions, have spherical and cylindrical shapes. This belief is due, in part, to the success of phenomenologically based theories for micelles that assume spherical and cylindrical shapes for the aggregates. These theories predict simple forms for the size and shape distributions of micelles that have not been confirmed directly, by experiment or by previous computer simulations. By conducting large-scale simulations of many thousands of surfactant molecules, it is found that one should monitor the aggregate size distribution carefully to determine when equilibrium is reached. In many previous studies, this was not done, and the reported size distributions were not truly representative of equilibrium values, and did not match the predictions of theory.
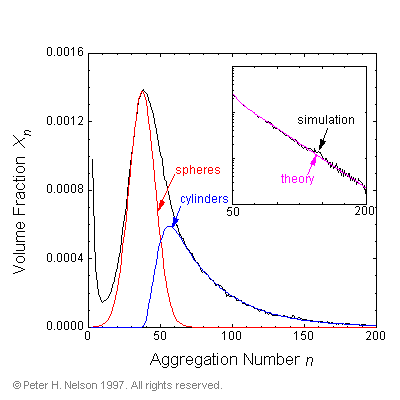
The mathematical forms of the size distributions reported here are found to closely correspond with the predictions of the phenomenological theories that assume spherical and cylindrical aggregate shapes (Fig. 6).
|
|
Fig. 6 Micellar size distribution fitted to the forms expected for spherical and cylindrical micelles in a 7.5% surfactant volume fraction simulation. Inset is the size distribution in the range n=50 to n=200 on a semi-log plot to show the exponential tail of the cylindrical micelles. |
This is somewhat surprising, as the self-assembled aggregates deviate significantly from the assumed shapes. The "spherical" micelles are not perfectly spherical, the short "cylindrical" micelles are not rigid cylinders but have a flexible worm-like structure, and finally the largest aggregates are not only highly flexible but can have one or more branch points (Fig 7).
|
|
Fig. 7 Micelles taken from a single snapshot of a 15% surfactant volume simulation. They have aggregation numbers of 42, 91, 125 and 269 (starting at the lower left and proceeding clockwise), also shown is a single surfactant molecule. |
Notwithstanding these deviations in actual structure from that assumed by the theoretical treatments, the accuracy with which the theoretical predictions follow the observed behavior is truly striking - indicating that the general approach of the phenomenological theories may actually be better than anticipated. This provides a new explanation for their success in predicting experimental behavior.
An estimate is also provided for how long a simulation should be run to representatively sample a size distribution at equilibrium. This estimate is based on the "dynamics" of the Monte Carlo simulation and is related to the rate at which single surfactant molecules desorb from a micelle. This estimate successfully predicts the increased time required to sample a broad size distribution in a (relatively) small sized simulation.
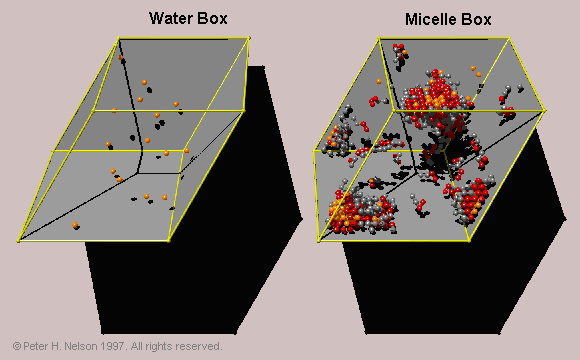
When oil is added to the surfactant simulation, there is an additional degree of freedom added to the system, which may allow coexisting phases to appear in the small simulation box. In order reduce the chance of this occurring, and to measure the oil partition coefficient between the micellar phase and a bulk aqueous solution, a two-box simulation method is developed. This method utilizes a thermodynamic ensemble for simulations, which I call the "Helmholtz" ensemble.
|
|
Fig. 8 Two-box simulation within the Helmholtz ensemble. The water box contains water and oil. The micelle box contains oil, water and surfactant. Oil and water molecules can exchange between the two simulation boxes with the constraint that the volume of the boxes does not change. |
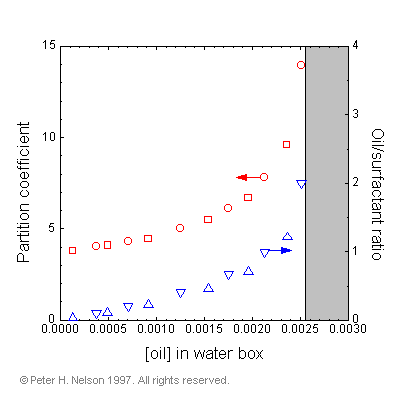
The name signifies that for each box the variables (T,V) are specified. This can be compared with the previously developed "Gibbs ensemble" where (T,P) can be specified. This ensemble is shown to be useful for investigating coexisting phases in lattice simulations and is also applicable to off-lattice simulations. The Helmholtz ensemble is used with two constant volume boxes at the same temperature: a micelle box containing oil, water and surfactant; and a water box containing just oil and water. In the simulation, oil and water can exchange between the two boxes at constant system volume. A significant advantage of this method is that we can directly measure the equilibrium concentration of oil in the water box, and hence the partition coefficient (Fig. 9).
|
|
Fig. 9 Partition coefficient of oil between a 7.5% surfactant volume micellar solution and bulk water phase, as a function of oil concentration in the water phase. Circles are from a larger system (40x40x40) and squares are from a smaller system (20x20x20). Also shown are the total oil/surfactant ratios in the two-box simulation. The shaded region indicates the phase boundary for emulsification failure. |
As long as this concentration is below the solubility limit for the oil in water, we are guaranteed that the system is stable with respect to emulsification failure (or the appearance of a bulk oil phase). Such guarantees concerning phase behavior are impossible using the traditional single box simulation method in the canonical ensemble.
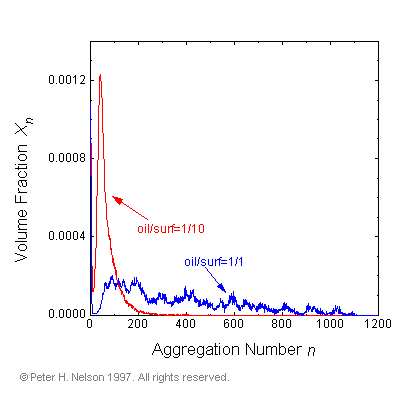
The effect of solubilized oil on the equilibrium microstructure of a dilute micellar system is investigated for the first time. It is found that small amounts of solubilized oil produce dramatic growth of the micelles (Fig. 10).
|
|
Fig. 10 Micellar growth. Comparison of micellar size distributions in two-box simulations with oil/surfactant molecular ratios of 1/10 and 1/1. |
Asymmetric growth upon addition of oil, has previously been proposed as an explanation for experimentally observed changes in the macroscopic phase behavior of dilute surfactant solutions as oil was added. The proposal was based on a phenomenological model of surfactant behavior based on the "packing factor". It was not based on any direct measurements of the changes in the microstructure of the surfactant solutions. The simulation results therefore serve to confirm not only the microscopic interpretation of the macroscopic phase behavior, but also the phenomenological model that the microscopic interpretation was based on. The packing factor is a concept used to predict the preferred interfacial curvature for a surfactant in a complex liquid. It is the ratio of the effective surfactant tail cross-sectional area to the effective head cross-sectional area. The local environment of the tails is important in determining the packing factor.
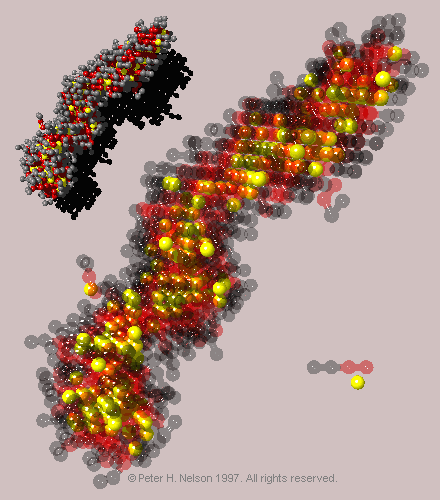
As oil is added to the system, it is preferentially absorbed into the tail region of the micelles (Fig. 11), reducing the local tail concentration in the core of the micelle, and thus increasing the effective cross-sectional area of the tails.
|
|
Fig. 11 Snapshot of a micellar aggregate of n=271 surfactants taken from a two-box simulation with an oil/surfactant molecular ratio of 1/1. Upper left - micelle shown with solid beads. Center - micelle shown with translucent surfactant beads to show the location of the oil (yellow) in the tail (red) regions of the micelle. Also shown are single surfactant and oil molecules. |
The packing factor is then increased and the surfactant prefers interfaces with lower overall curvature - such as the worm-like structures observed in the simulation. This phenomenological model does not yet appear to have gained widespread use.
Circle4.com